押川研究室

これまでの研究成果（+余談）- 第2部

粒子密度の整合性条件 (Lieb-Schultz-Mattis定理の一般化）

上で触れた「隠れた対称性の一般化」論文の中で、部分的に磁化したAKLT状態を構成して、その状態における隠れた対称性の破れを 論じました。

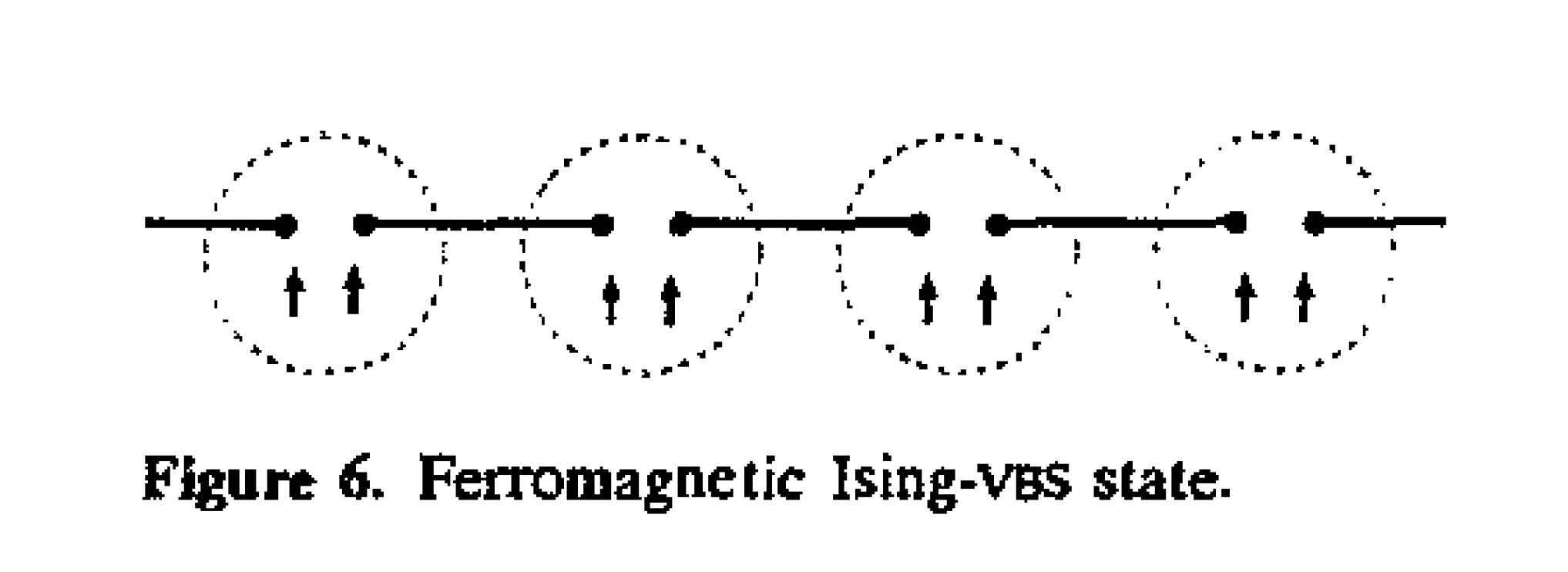
それは計算すればできたのですが、「部分的に磁化したAKLT状態」（に近い状態）が物理的にどのような状況で 実現されるのかが気になっていました。予想としては、スピン鎖に磁場をかけたとき、磁化過程の中で現れると思ったのですが、 その意義については混乱したままでした。 当時同じ甲元研にいた山中雅則君とも議論していましたが、そのときはどう理解するべきなのか良くわかりませんでした。

1995年秋から、Ian Affleckのポスドクとしてカナダ・バンクーバーのUniversity of British Columbia (UBC)に行きました。 ↑の、部分的に磁化したAKLT状態の話を相談すると、それはLieb-Schultz-Mattis (LSM)定理に関係するんじゃないか、 とすぐに示唆してくれました。 そこから、U(1)対称性を持つ量子スピン鎖で励起ギャップを持つ「磁化プラトー」が出現するための量子化条件がすぐに導かれました↓

Masaki Oshikawa, Masanori Yamanaka, and Ian Affleck, Magnetization Plateaus in Spin Chains: "Haldane Gap" for Half-Integer Spins Phys. Rev. Lett. 78, 1984 (1997) ,
arXiv:cond-mat/9610168 [被引用件数:831] (2023/4)

その後、LSM定理は（技術的には何の困難もなく）電子系にも適用でき 固体電子論の基本であるLuttinger定理の非摂動論的な「証明」を与えることもわかりました↓

Masanori Yamanaka, Masaki Oshikawa, and Ian Affleck, Nonperturbative Approach to Luttinger's Theorem in One Dimension, Phys. Rev. Lett. 79, 1110 (1997) ,
arXiv:cond-mat/9701141 [被引用件数:209] (2023/4)

電子系にも適用してみると、LSM定理の本質は粒子密度と格子の「整合性」にあることがはっきりします。 ミステリアスだったHaldane予想（整数スピン鎖と半奇数スピン鎖の差異）も、 量子スピン鎖を多粒子系と解釈すれば整合性条件の帰結に他なりません。 直観的には、整合性条件は次元によらず重要なはずです。 そこで、LSM定理を高次元に拡張することを考えました。 LSMの原論文の最後の方に、サイズが異方的な極限（縦と横を同時に無限大にするが、縦横比がゼロに近づくようにする） ではLSMの1次元的な証明が高次元系に適用できることはコメントされているのですが、そういうめっちゃ細長い系を 高次元系とみなして良いのかはよくわかりませんでした。 （今から振り返ってみると、本質的にはそれでも良かった気もします。まあ、これは、 サイズが等方的な高次元系でちゃんと示されたので、そうも思えるのでしょう。）

しばらく糸口がつかめなかったのですが、Laughlinが量子ホール効果でホール伝導度が量子化されることを示す 議論に用いた、Aharonov-Bohm磁束の断熱挿入を考えればよい、とふと思いつきました。 （UBCにいた頃から考えていましたが、これを思いついたのは東工大に移ってからです。） それで書いたのが↓です。

Masaki Oshikawa, Commensurability, Excitation Gap, and Topology in Quantum Many-Particle Systems on a Periodic Lattice, Phys. Rev. Lett. 84, 1535 (2000),
arXiv:cond-mat/9911137 [被引用件数:396] (2023/4)

この話はAharonov-Bohm磁束の挿入でギャップが閉じない（物理的にはリーズナブルだが非自明な）仮定に依存しているので ちゃんとした証明ではありませんが、その後Hastingsらによって厳密な証明が与えられています。 （Lieb-Schultz-Mattis-Oshikawa-Hastings theoremと呼ばれることもあります。） 一方、ここで使ったflux insertion argumentはいろいろと応用ができて、この後何度も役に立ちます。 まず、"flux insertion argument"でやはり一般次元のLuttingerの定理の非摂動的な「証明」もできる、 というのが↓の論文です。

Masaki Oshikawa, Topological Approach to Luttinger's Theorem and the Fermi Surface of a Kondo Lattice, Phys. Rev. Lett. 84, 3370 (2000),
arXiv:cond-mat/0002392 [被引用件数:313] (2023/4)

この話は、Subir Sachdev氏の講義や、 同氏による最近の教科書Quantum Phases of Matterでもかなり丁寧に解説して頂いています。

一般化されたLSM定理、あるいは整合性条件による制約、は2010年代以降ふたたび盛んに研究され、さまざまに拡張されています。 LSM原論文の議論の現代的な解説は田崎さんの教科書 Physics and Mathematics of Quantum Many-Body Systems (Graduate Texts in Physics)が、 最近のさまざまな拡張に関する解説は、渡辺悠樹君による 量子多体系の対称性とトポロジー: 統一的な理解を目指して (SGCライブラリ 179)が良いと思います。 僕自身も関連する研究を最近もやっているので、また追記するかもしれません。